Chi-Square Test of Independence | Formula, Guide & Examples

Published on May 30, 2022 by Shaun Turney. Revised on July 15, 2022.

A chi-square (Χ²) test of independence is a nonparametric hypothesis test. You can use it to test whether two categorical variables are related to each other.

Example: Chi-square test of independence

Imagine a city wants to encourage more of its residents to recycle their household waste.

The city decides to test two interventions: an educational pamphlet or a phone call. They randomly select 300 households and randomly assign them to the pamphlet, phone call, or control (no intervention) group. They’ll use the results of their experiment to decide which intervention to use for the whole city.

The city plans to use a chi-square test of independence to test whether the proportion of households who recycle differs between the interventions.

What is the chi-square test of independence?
Chi-square test of independence hypotheses
When to use the chi-square test of independence
How to calculate the test statistic (formula)
How to perform the chi-square test of independence
When to use a different test
Practice questions
Frequently asked questions about the chi-square test of independence

What is the chi-square test of independence?

A chi-square (Χ²) test of independence is a type of Pearson’s chi-square test. Pearson’s chi-square tests are nonparametric tests for categorical variables. They’re used to determine whether your data are significantly different from what you expected.

You can use a chi-square test of independence, also known as a chi-square test of association, to determine whether two categorical variables are related. If two variables are related, the probability of one variable having a certain value is dependent on the value of the other variable.

Note: You can say that you’re testing whether the variables are related, associated, contingent, or dependent—these are all synonyms.

The chi-square test of independence calculations are based on the observed frequencies, which are the numbers of observations in each combined group.

The test compares the observed frequencies to the frequencies you would expect if the two variables are unrelated. When the variables are unrelated, the observed and expected frequencies will be similar.

Contingency tables

When you want to perform a chi-square test of independence, the best way to organize your data is a type of frequency distribution table called a contingency table.

A contingency table, also known as a cross tabulation or crosstab, shows the number of observations in each combination of groups. It also usually includes row and column totals.

Contingency-table-bar-graph — Example: Contingency table

Household address	Intervention	Outcome
25 Elm Street	Pamphlet	Recycles
100 Cedar Street	Control	Recycles
3 Maple Street	Control	Does not recycle
123 Oak Street	Phone call	Recycles
…	…	…

Intervention	Recycles	Does not recycle	Row totals
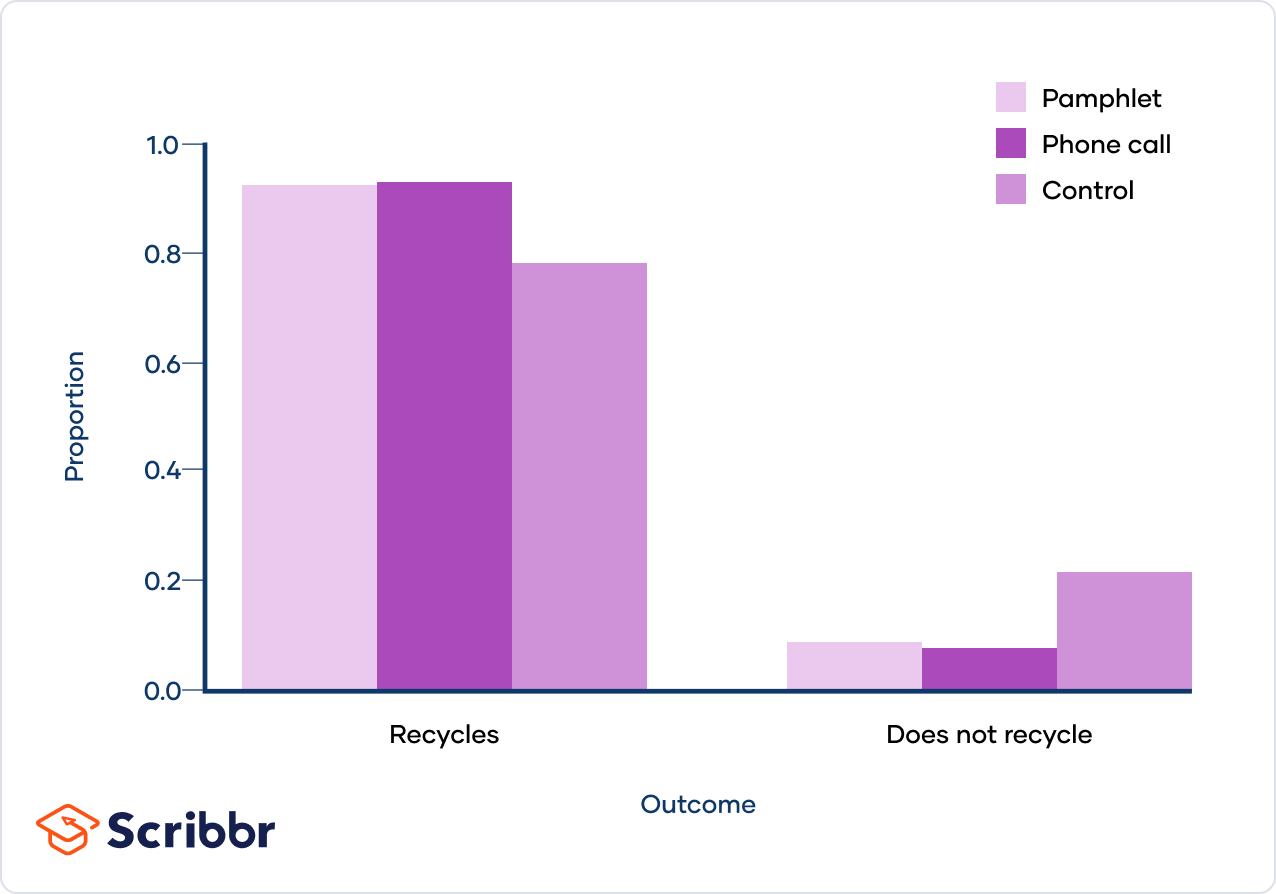
Pamphlet	89	9	98
Phone call	84	8	92
Control	86	24	110
Column totals	259	41	N = 300

Chi-square test of independence hypotheses

The chi-square test of independence is an inferential statistical test, meaning that it allows you to draw conclusions about a population based on a sample. Specifically, it allows you to conclude whether two variables are related in the population.

Like all hypothesis tests, the chi-square test of independence evaluates a null and alternative hypothesis. The hypotheses are two competing answers to the question “Are variable 1 and variable 2 related?”

Null hypothesis (H₀): Variable 1 and variable 2 are not related in the population; The proportions of variable 1 are the same for different values of variable 2.
Alternative hypothesis (H_a): Variable 1 and variable 2 are related in the population; The proportions of variable 1 are not the same for different values of variable 2.

You can use the above sentences as templates. Replace variable 1 and variable 2 with the names of your variables.

Example: Null & alternative hypotheses

The population is all households in the city.

Null hypothesis (H₀): Whether a household recycles and the type of intervention they receive are not related in the population; The proportion of households that recycle is the same for all interventions.
Alternative hypothesis (H_a): Whether a household recycles and the type of intervention they receive are related in the population; The proportion of households that recycle is not the same for all interventions.

Expected values

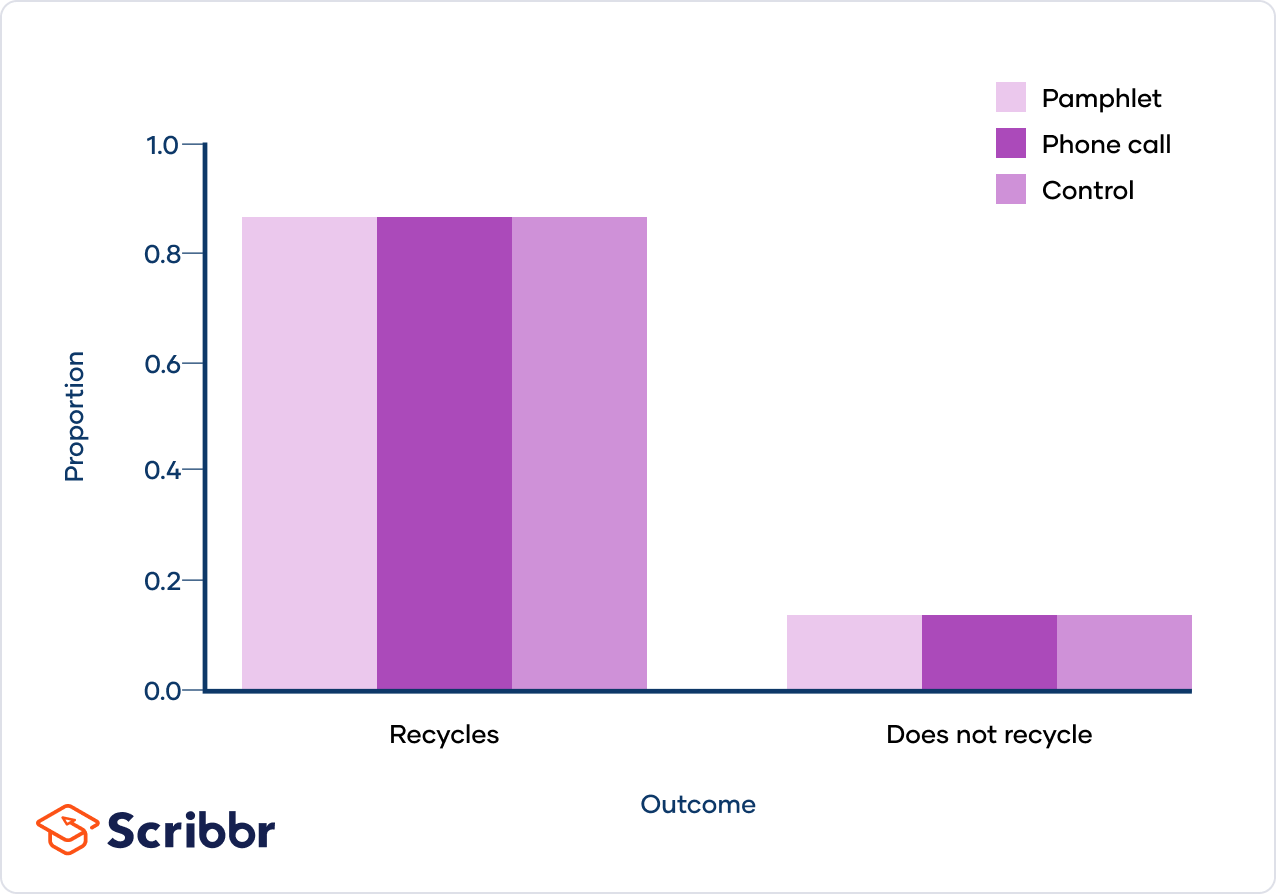
A chi-square test of independence works by comparing the observed and the expected frequencies. The expected frequencies are such that the proportions of one variable are the same for all values of the other variable.

You can calculate the expected frequencies using the contingency table. The expected frequency for row r and column c is:

$\begin{equation*}\dfrac{(\textup{Row}\,\, r \,\,\textup{total}\,\, \times \textup{Column}\,\, c \,\,\textup{total})}{N}\end{equation*}$

Example: Expected values

The city calculates the expected frequencies using the contingency table.

Observed and expected frequencies (observed above, expected below)
Intervention	Recycles	Does not recycle	Row totals
Pamphlet	$89$	$9$	$98$
Pamphlet	$\dfrac{(98\times259)}{300}=84.61$	$\dfrac{(98\times41)}{300}=13.39$	$98$
Phone call	$84$	$8$	$92$
Phone call	$\dfrac{(92\times259)}{300}=79.43$	$\dfrac{(92\times41)}{300}=12.57$	$92$
Control	$86$	$24$	$110$
Control	$\dfrac{(110\times259)}{300}=94.97$	$\dfrac{(110\times41)}{300}=15.03$	$110$
Column totals	$259$	$41$	$N=300$

The expected frequencies are such that the proportion of households who recycle is the same for all interventions:

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

When to use the chi-square test of independence

The following conditions are necessary if you want to perform a chi-square goodness of fit test:

You want to test a hypothesis about the relationship between two categorical variables (binary, nominal, or ordinal).
- Chi-square tests of independence are usually performed on binary or nominal variables. They are sometimes performed on ordinal variables, although generally only on ordinal variables with fewer than five groups.
The sample was randomly selected from the population.
There are a minimum of five observations expected in each combined group.

Example: Chi-square test of independence conditions

The city can use a chi-square goodness of fit test to analyze the recycling intervention data because all three conditions have been met:

They want to test a hypothesis about the relationships between two categorical variables: whether a household recycles and the type of intervention.
They recruited a random sample of 300 households.
There are a minimum of five observations expected in each combined group. The smallest expected frequency is 12.57.

How to calculate the test statistic (formula)

Pearson’s chi-square (Χ²) is the test statistic for the chi-square test of independence:

$\begin{equation*}X^2 = \sum {\frac {(O-E)^2}{E}}$\end{equation*}$

Where

Χ² is the chi-square test statistic
Σ is the summation operator (it means “take the sum of”)
O is the observed frequency
E is the expected frequency

The chi-square test statistic measures how much your observed frequencies differ from the frequencies you would expect if the two variables are unrelated. It is large when there’s a big difference between the observed and expected frequencies (O − E in the equation).

Follow these five steps to calculate the test statistic:

Step 1: Create a table

Create a table with the observed and expected frequencies in two columns.

Example: Step 1

Intervention	Outcome	Observed	Expected
Pamphlet	Recycles	89	84.61
Pamphlet	Does not recycle	9	13.39
Phone call	Recycles	84	79.43
Phone call	Does not recycle	8	12.57
Control	Recycles	86	94.97
Control	Does not recycle	24	15.03

Step 2: Calculate O − E

In a new column called “O − E”, subtract the expected frequencies from the observed frequencies.

Example: Step 2

Intervention	Outcome	Observed	Expected	O − E
Pamphlet	Recycles	89	84.61	4.39
Pamphlet	Does not recycle	9	13.39	-4.39
Phone call	Recycles	84	79.43	4.57
Phone call	Does not recycle	8	12.57	-4.57
Control	Recycles	86	94.97	-8.97
Control	Does not recycle	24	15.03	8.97

Step 3: Calculate (O – E)²

In a new column called “(O − E)²”, square the values in the previous column.

Example: Step 3

Intervention	Outcome	Observed	Expected	O − E	(O − E)²
Pamphlet	Recycles	89	84.61	4.39	19.27
Pamphlet	Does not recycle	9	13.39	-4.39	19.27
Phone call	Recycles	84	79.43	4.57	20.88
Phone call	Does not recycle	8	12.57	-4.57	20.88
Control	Recycles	86	94.97	-8.97	80.46
Control	Does not recycle	24	15.03	8.97	80.46

Step 4: Calculate (O − E)² / E

In a final column called “(O − E)² / E”, divide the previous column by the expected frequencies.

Example: Step 4

Intervention	Outcome	Observed	Expected	O − E	(O − E)²	(O − E)² / E
Pamphlet	Recycles	89	84.61	4.39	19.27	0.23
Pamphlet	Does not recycle	9	13.39	-4.39	19.27	1.44
Phone call	Recycles	84	79.43	4.57	20.88	0.26
Phone call	Does not recycle	8	12.57	-4.57	20.88	1.66
Control	Recycles	86	94.97	-8.97	80.46	0.85
Control	Does not recycle	24	15.03	8.97	80.46	5.35

Step 5: Calculate Χ²

Finally, add up the values of the previous column to calculate the chi-square test statistic (Χ2).

Example: Step 5

Χ² = 0.23 + 1.44 + 0.26 + 1.66 + 0.85 + 5.35

Χ² = 9.79

How to perform the chi-square test of independence

If the test statistic is big enough then you should conclude that the observed frequencies are not what you’d expect if the variables are unrelated. But what counts as big enough?

We compare the test statistic to a critical value from a chi-square distribution to decide whether it’s big enough to reject the null hypothesis that the two variables are unrelated. This procedure is called the chi-square test of independence.

Follow these steps to perform a chi-square test of independence (the first two steps have already been completed for the recycling example):

Step 1: Calculate the expected frequencies

Use the contingency table to calculate the expected frequencies following the formula:

$\begin{equation*}\dfrac{(\textup{Row}\,\, r \,\,\textup{total}\,\, \times \textup{Column}\,\, c \,\,\textup{total})}{\textup{Grand}\,\, \textup{total}}\end{equation*}$

Step 2: Calculate chi-square

Use the Pearson’s chi-square formula to calculate the test statistic:

$\begin{equation*}X^2 = \sum {\frac {(O - E)^2}{E}}\end{equation*}$

Step 3: Find the critical chi-square value

You can find the critical value in a chi-square critical value table or using statistical software. You need to known two numbers to find the critical value:

The degrees of freedom (df): For a chi-square test of independence, the df is (number of variable 1 groups − 1) * (number of variable 2 groups − 1).
Significance level (α): By convention, the significance level is usually .05.

Example: Finding the critical chi-square value

Since there are three intervention groups (pamphlet, phone call, and control) and two outcome groups (recycle and does not recycle) there are (3 − 1) * (2 − 1) = 2 degrees of freedom.

For a test of significance at α = .05 and df = 2, the Χ² critical value is 5.99.

Step 4: Compare the chi-square value to the critical value

Is the test statistic big enough to reject the null hypothesis? Compare it to the critical value to find out.

Example: Comparing the chi-square value to the critical value

Χ² = 9.79

Critical value = 5.99

The Χ² value is greater than the critical value.

Step 5: Decide whether to reject the null hypothesis

If the Χ² value is greater than the critical value, then the difference between the observed and expected distributions is statistically significant (p < α).
- The data allows you to reject the null hypothesis that the variables are unrelated and provides support for the alternative hypothesis that the variables are related.
If the Χ² value is less than the critical value, then the difference between the observed and expected distributions is not statistically significant (p > α).
- The data doesn’t allow you to reject the null hypothesis that the variables are unrelated and doesn’t provide support for the alternative hypothesis that the variables are related.

Example: Deciding whether to reject the null hypothesis

The Χ² value is greater than the critical value. Therefore, the city rejects the null hypothesis that whether a household recycles and the type of intervention they receive are unrelated.

There is a significant difference between the observed frequencies and the frequencies expected if the two variables were unrelated (p < .05). This suggests that the proportion of households that recycle is not the same for all interventions.

The city concludes that their interventions have an effect on whether households choose to recycle.

Step 6: Follow up with post hoc tests (optional)

If there are more than two groups in either of the variables and you rejected the null hypothesis, you may want to investigate further with post hoc tests. A post hoc test is a follow-up test that you perform after your initial analysis.

Similar to a one-way ANOVA with more than two groups, a significant difference doesn’t tell you which groups’ proportions are significantly different from each other.

One post hoc approach is to compare each pair of groups using chi-square tests of independence and a Bonferroni correction. A Bonferroni correction is when you divide your original significance level (usually .05) by the number of tests you’re performing.

Example: Post hoc tests

Although the city now knows that the proportion of households recycling is not the same for all interventions, they don’t know which interventions differ from each other. To find out, they perform post hoc tests, comparing each pair of interventions using a chi-square test of independence.

Chi-square test of independence	Chi-square test statistic
Pamphlet vs. phone call	0.014
Pamphlet vs. control	6.198
Phone call vs. control	6.471

Since there are two intervention groups and two outcome groups for each test, there is (2 − 1) * (2 − 1) = 1 degree of freedom.
There are three tests, so the significance level with a Bonferroni correction applied is α = .05 / 3 = .016.
For a test of significance at α = .016 and df = 1, the Χ² critical value is 5.803.
The chi-square value is greater than the critical value for the pamphlet vs control and phone call vs. control tests.

Based on these findings, the city concludes that a significantly greater proportion of households recycled after receiving a pamphlet or phone call compared to the control.

There was no significant difference in proportion between the pamphlet and phone call intervention, so the city chooses the phone call intervention because it creates less paper waste.

When to use a different test

Several tests are similar to the chi-square test of independence, so it may not always be obvious which to use. The best choice will depend on your variables, your sample size, and your hypotheses.

When to use the chi-square goodness of fit test

There are two types of Pearson’s chi-square test. The chi-square test of independence is one of them, and the chi-square goodness of fit test is the other. The math is the same for both tests—the main difference is how you calculate the expected values.

You should use the chi-square goodness of fit test when you have one categorical variable and you want to test a hypothesis about its distribution.

When to use Fisher’s exact test

If you have a small sample size (N < 100), Fisher’s exact test is a better choice. You should especially opt for Fisher’s exact test when your data doesn’t meet the condition of a minimum of five observations expected in each combined group.

When to use McNemar’s test

You should use McNemar’s test when you have a closely-related pair of categorical variables that each have two groups. It allows you to test whether the proportions of the variables are equal. This test is most often used to compare before and after observations of the same individuals.

When to use a G test

A G test and a chi-square test give approximately the same results. G tests can accommodate more complex experimental designs than chi-square tests. However, the tests are usually interchangeable and the choice is mostly a matter of personal preference.

One reason to prefer chi-square tests is that they’re more familiar to researchers in most fields.

Practice questions

Do you want to test your knowledge about the chi-square goodness of fit test? Download our practice questions and examples with the buttons below.

Download Word doc Download Google doc

Frequently asked questions about the chi-square test of independence

How do I perform a chi-square test of independence in Excel?: You can use the CHISQ.TEST() function to perform a chi-square test of independence in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value.
How do I perform a chi-square test of independence in R?: You can use the chisq.test() function to perform a chi-square test of independence in R. Give the contingency table as a matrix for the “x” argument. For example:

m = matrix(data = c(89, 84, 86, 9, 8, 24), nrow = 3, ncol = 2)

chisq.test(x = m)
What are the two main types of chi-square tests?: The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence.
What properties does the chi-square distribution have?: A chi-square distribution is a continuous probability distribution. The shape of a chi-square distribution depends on its degrees of freedom, k. The mean of a chi-square distribution is equal to its degrees of freedom (k) and the variance is 2k. The range is 0 to ∞.

Sources in this article

We strongly encourage students to use sources in their work. You can cite our article (APA Style) or take a deep dive into the articles below.

This Scribbr article

Turney, S. (July 15, 2022). Chi-Square Test of Independence | Formula, Guide & Examples. Scribbr. Retrieved October 17, 2022, from https://www.scribbr.com/statistics/chi-square-test-of-independence/

Cite this article

Is this article helpful?

You have already voted. Thanks :-) Your vote is saved :-) Processing your vote...

Shaun Turney

During his MSc and PhD, Shaun learned how to apply scientific and statistical methods to his research in ecology. Now he loves to teach students how to collect and analyze data for their own theses and research projects.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes

Generate accurate citations for free