Chi-Square Goodness of Fit Test | Formula, Guide & Examples
A chi-square (Χ2) goodness of fit test is a type of Pearson’s chi-square test. You can use it to test whether the observed distribution of a categorical variable differs from your expectations.
You recruit a random sample of 75 dogs and offer each dog a choice between the three flavors by placing bowls in front of them. You expect that the flavors will be equally popular among the dogs, with about 25 dogs choosing each flavor.
Once you have your experimental results, you plan to use a chi-square goodness of fit test to figure out whether the distribution of the dogs’ flavor choices is significantly different from your expectations.
The chi-square goodness of fit test tells you how well a statistical model fits a set of observations. It’s often used to analyze genetic crosses.
Table of contents
- What is the chi-square goodness of fit test?
- Chi-square goodness of fit test hypotheses
- When to use the chi-square goodness of fit test
- How to calculate the test statistic (formula)
- How to perform the chi-square goodness of fit test
- When to use a different test
- Practice questions and examples
- Frequently asked questions about the chi-square goodness of fit test
What is the chi-square goodness of fit test?
A chi-square (Χ2) goodness of fit test is a goodness of fit test for a categorical variable. Goodness of fit is a measure of how well a statistical model fits a set of observations.
- When goodness of fit is high, the values expected based on the model are close to the observed values.
- When goodness of fit is low, the values expected based on the model are far from the observed values.
The statistical models that are analyzed by chi-square goodness of fit tests are distributions. They can be any distribution, from as simple as equal probability for all groups, to as complex as a probability distribution with many parameters.
Hypothesis testing
The chi-square goodness of fit test is a hypothesis test. It allows you to draw conclusions about the distribution of a population based on a sample. Using the chi-square goodness of fit test, you can test whether the goodness of fit is “good enough” to conclude that the population follows the distribution.
With the chi-square goodness of fit test, you can ask questions such as: Was this sample drawn from a population that has…
- Equal proportions of male and female turtles?
- Equal proportions of red, blue, yellow, green, and purple jelly beans?
- 90% right-handed and 10% left-handed people?
- Offspring with an equal probability of inheriting all possible genotypic combinations (i.e., unlinked genes)?
- A Poisson distribution of floods per year?
- A normal distribution of bread prices?
| Flavor | Observed | Expected |
| Garlic Blast | 22 | 25 |
| Blueberry Delight | 30 | 25 |
| Minty Munch | 23 | 25 |
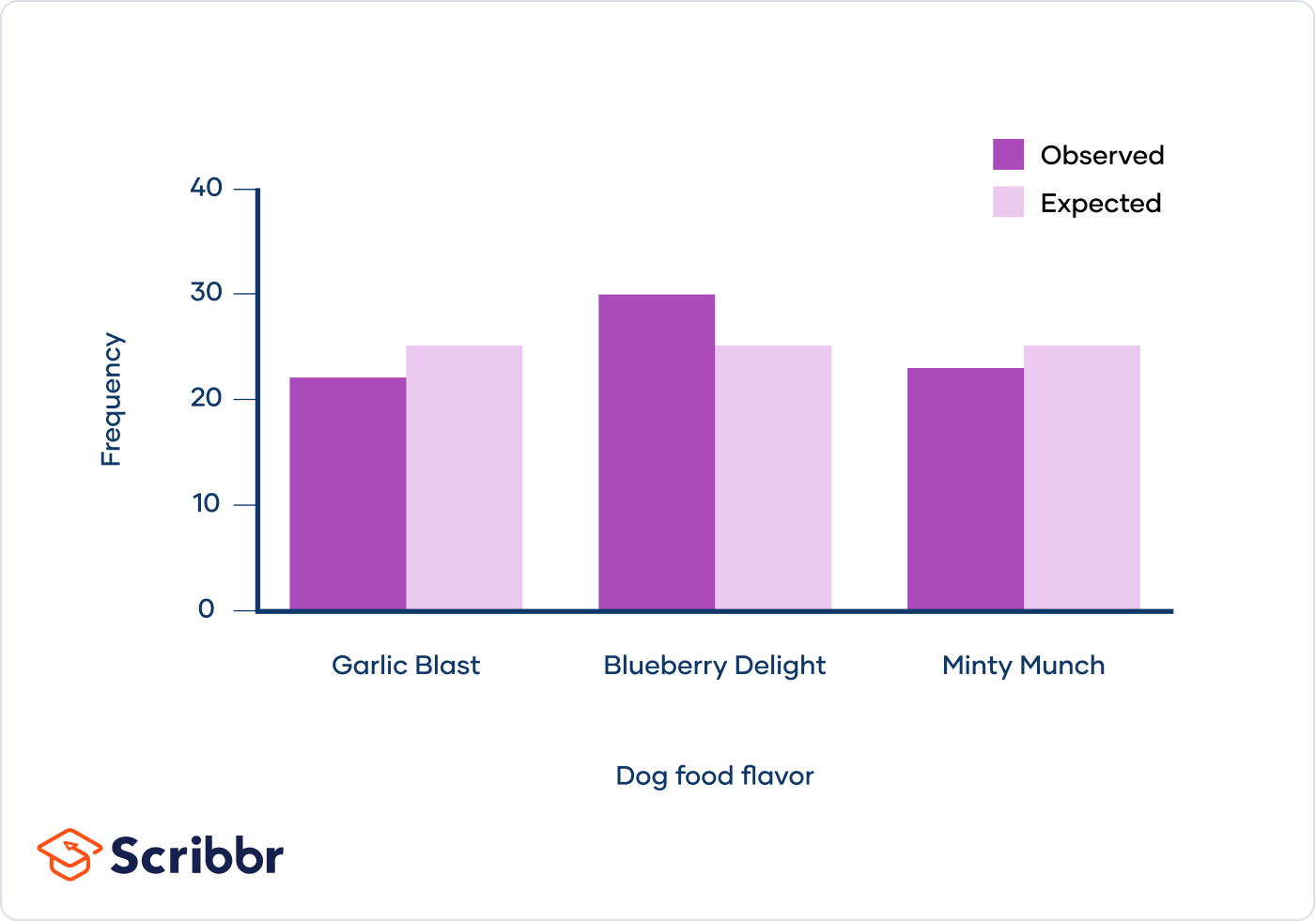
To help visualize the differences between your observed and expected frequencies, you also create a bar graph:
The president of the dog food company looks at your graph and declares that they should eliminate the Garlic Blast and Minty Munch flavors to focus on Blueberry Delight. “Not so fast!” you tell him.
You explain that your observations were a bit different from what you expected, but the differences aren’t dramatic. They could be the result of a real flavor preference or they could be due to chance.
To put it another way: You have a sample of 75 dogs, but what you really want to understand is the population of all dogs. Was this sample drawn from a population of dogs that choose the three flavors equally often?
Chi-square goodness of fit test hypotheses
Like all hypothesis tests, a chi-square goodness of fit test evaluates two hypotheses: the null and alternative hypotheses. They’re two competing answers to the question “Was the sample drawn from a population that follows the specified distribution?”
- Null hypothesis (H0): The population follows the specified distribution.
- Alternative hypothesis (Ha): The population does not follow the specified distribution.
These are general hypotheses that apply to all chi-square goodness of fit tests. You should make your hypotheses more specific by describing the “specified distribution.” You can name the probability distribution (e.g., Poisson distribution) or give the expected proportions of each group.
- Null hypothesis (H0): The dog population chooses the three flavors in equal proportions (p1 = p2 = p3).
- Alternative hypothesis (Ha): The dog population does not choose the three flavors in equal proportions.
Here's why students love Scribbr's proofreading services
When to use the chi-square goodness of fit test
The following conditions are necessary if you want to perform a chi-square goodness of fit test:
- You want to test a hypothesis about the distribution of one categorical variable. If your variable is continuous, you can convert it to a categorical variable by separating the observations into intervals. This process is known as data binning.
- The sample was randomly selected from the population.
- There are a minimum of five observations expected in each group.
- You want to test a hypothesis about the distribution of one categorical variable. The categorical variable is the dog food flavors.
- You recruited a random sample of 75 dogs.
- There were a minimum of five observations expected in each group. For all three dog food flavors, you expected 25 observations of dogs choosing the flavor.
How to calculate the test statistic (formula)
The test statistic for the chi-square (Χ2) goodness of fit test is Pearson’s chi-square:
| Formula | Explanation |
|---|---|
|
The larger the difference between the observations and the expectations (O − E in the equation), the bigger the chi-square will be.
To use the formula, follow these five steps:
Step 1: Create a table
Create a table with the observed and expected frequencies in two columns.
| Flavor | Observed | Expected |
| Garlic Blast | 22 | 25 |
| Blueberry Delight | 30 | 25 |
| Minty Munch | 23 | 25 |
Step 2: Calculate O − E
Add a new column called “O − E”. Subtract the expected frequencies from the observed frequency.
| Flavor | Observed | Expected | O − E |
| Garlic Blast | 22 | 25 | 22 − 25 = −3 |
| Blueberry Delight | 30 | 25 | 5 |
| Minty Munch | 23 | 25 | −2 |
Step 3: Calculate (O − E)2
Add a new column called “(O − E)2”. Square the values in the previous column.
| Flavor | Observed | Expected | O − E | (O − E)2 |
| Garlic Blast | 22 | 25 | −3 | (−3)2 = 9 |
| Blueberry Delight | 30 | 25 | 5 | 25 |
| Minty Munch | 23 | 25 | −2 | 4 |
Step 4: Calculate (O − E)2 / E
Add a final column called “(O − E)² / E“. Divide the previous column by the expected frequencies.
| Flavor | Observed | Expected | O − E | (O − E)2 | (O − E)² / E |
| Garlic Blast | 22 | 25 | −3 | 9 | 9/25 = 0.36 |
| Blueberry Delight | 30 | 25 | 5 | 25 | 1 |
| Minty Munch | 23 | 25 | −2 | 4 | 0.16 |
Step 5: Calculate Χ2
Add up the values of the previous column. This is the chi-square test statistic (Χ2).
| Flavor | Observed | Expected | O − E | (O − E)2 | (O − E)2 / E |
| Garlic Blast | 22 | 25 | −3 | 9 | 9/25 = 0.36 |
| Blueberry Delight | 30 | 25 | 5 | 25 | 1 |
| Minty Munch | 23 | 25 | −2 | 4 | 0.16 |
Χ2 = 0.36 + 1 + 0.16 = 1.52
How to perform the chi-square goodness of fit test
The chi-square statistic is a measure of goodness of fit, but on its own it doesn’t tell you much. For example, is Χ2 = 1.52 a low or high goodness of fit?
To interpret the chi-square goodness of fit, you need to compare it to something. That’s what a chi-square test is: comparing the chi-square value to the appropriate chi-square distribution to decide whether to reject the null hypothesis.
To perform a chi-square goodness of fit test, follow these five steps (the first two steps have already been completed for the dog food example):
Step 1: Calculate the expected frequencies
Sometimes, calculating the expected frequencies is the most difficult step. Think carefully about which expected values are most appropriate for your null hypothesis.
In general, you’ll need to multiply each group’s expected proportion by the total number of observations to get the expected frequencies.
Step 2: Calculate chi-square
Calculate the chi-square value from your observed and expected frequencies using the chi-square formula.
Step 3: Find the critical chi-square value
Find the critical chi-square value in a chi-square critical value table or using statistical software. The critical value is calculated from a chi-square distribution. To find the critical chi-square value, you’ll need to know two things:
- The degrees of freedom (df): For chi-square goodness of fit tests, the df is the number of groups minus one.
- Significance level (α): By convention, the significance level is usually .05.
For a test of significance at α = .05 and df = 2, the Χ2 critical value is 5.99.
Step 4: Compare the chi-square value to the critical value
Compare the chi-square value to the critical value to determine which is larger.
Critical value = 5.99
The Χ2 value is less than the critical value.
Step 5: Decide whether the reject the null hypothesis
- If the Χ2 value is greater than the critical value, then the difference between the observed and expected distributions is statistically significant (p < α).
- The data allows you to reject the null hypothesis and provides support for the alternative hypothesis.
- If the Χ2 value is less than the critical value, then the difference between the observed and expected distributions is not statistically significant (p > α).
- The data doesn’t allow you to reject the null hypothesis and doesn’t provide support for the alternative hypothesis.
You report your findings back to the dog food company president. He decides not to eliminate the Garlic Blast and Minty Munch flavors based on your findings. The many dogs who love these flavors are very grateful!
When to use a different test
Whether you use the chi-square goodness of fit test or a related test depends on what hypothesis you want to test and what type of variable you have.
When to use the chi-square test of independence
There’s another type of chi-square test, called the chi-square test of independence.
- Use the chi-square goodness of fit test when you have one categorical variable and you want to test a hypothesis about its distribution.
- Use the chi-square test of independence when you have two categorical variables and you want to test a hypothesis about their relationship.
When to use a different goodness of fit test
The Anderson–Darling and Kolmogorov–Smirnov goodness of fit tests are two other common goodness of fit tests for distributions.
- Use the Anderson–Darling or the Kolmogorov–Smirnov goodness of fit test when you have a continuous variable (that you don’t want to bin).
- Use the chi-square goodness of fit test when you have a categorical variable (or a continuous variable that you want to bin).
Specialized goodness of fit tests are usually more powerful, so they’re often the best choice when a specialized test is available for the distribution you’re interested in.
Practice questions and examples
Do you want to test your knowledge about the chi-square goodness of fit test? Download our practice questions and examples with the buttons below.
Download Word doc Download Google doc
Frequently asked questions about the chi-square goodness of fit test
- How do I perform a chi-square goodness of fit test in Excel?
-
You can use the CHISQ.TEST() function to perform a chi-square goodness of fit test in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value.
- How do I perform a chi-square goodness of fit test in R?
-
You can use the chisq.test() function to perform a chi-square goodness of fit test in R. Give the observed values in the “x” argument, give the expected values in the “p” argument, and set “rescale.p” to true. For example:
chisq.test(x = c(22,30,23), p = c(25,25,25), rescale.p = TRUE)
- How do I perform a chi-square goodness of fit test for a genetic cross?
-
Chi-square goodness of fit tests are often used in genetics. One common application is to check if two genes are linked (i.e., if the assortment is independent). When genes are linked, the allele inherited for one gene affects the allele inherited for another gene.
Suppose that you want to know if the genes for pea texture (R = round, r = wrinkled) and color (Y = yellow, y = green) are linked. You perform a dihybrid cross between two heterozygous (RY / ry) pea plants. The hypotheses you’re testing with your experiment are:
- Null hypothesis (H0): The population of offspring have an equal probability of inheriting all possible genotypic combinations.
- This would suggest that the genes are unlinked.
- Alternative hypothesis (Ha): The population of offspring do not have an equal probability of inheriting all possible genotypic combinations.
- This would suggest that the genes are linked.
You observe 100 peas:
- 78 round and yellow peas
- 6 round and green peas
- 4 wrinkled and yellow peas
- 12 wrinkled and green peas
Step 1: Calculate the expected frequencies
To calculate the expected values, you can make a Punnett square. If the two genes are unlinked, the probability of each genotypic combination is equal.
RY ry Ry rY RY RRYY RrYy RRYy RrYY ry RrYy rryy Rryy rrYy Ry RRYy Rryy RRyy RrYy rY RrYY rrYy RrYy rrYY The expected phenotypic ratios are therefore 9 round and yellow: 3 round and green: 3 wrinkled and yellow: 1 wrinkled and green.
From this, you can calculate the expected phenotypic frequencies for 100 peas:
Phenotype Observed Expected Round and yellow 78 100 * (9/16) = 56.25 Round and green 6 100 * (3/16) = 18.75 Wrinkled and yellow 4 100 * (3/16) = 18.75 Wrinkled and green 12 100 * (1/16) = 6.21 Step 2: Calculate chi-square
Phenotype Observed Expected O − E (O − E)2 (O − E)2 / E Round and yellow 78 56.25 21.75 473.06 8.41 Round and green 6 18.75 −12.75 162.56 8.67 Wrinkled and yellow 4 18.75 −14.75 217.56 11.6 Wrinkled and green 12 6.21 5.79 33.52 5.4 Χ2 = 8.41 + 8.67 + 11.6 + 5.4 = 34.08
Step 3: Find the critical chi-square value
Since there are four groups (round and yellow, round and green, wrinkled and yellow, wrinkled and green), there are three degrees of freedom.
For a test of significance at α = .05 and df = 3, the Χ2 critical value is 7.82.
Step 4: Compare the chi-square value to the critical value
Χ2 = 34.08
Critical value = 7.82
The Χ2 value is greater than the critical value.
Step 5: Decide whether the reject the null hypothesis
The Χ2 value is greater than the critical value, so we reject the null hypothesis that the population of offspring have an equal probability of inheriting all possible genotypic combinations. There is a significant difference between the observed and expected genotypic frequencies (p < .05).
The data supports the alternative hypothesis that the offspring do not have an equal probability of inheriting all possible genotypic combinations, which suggests that the genes are linked
- Null hypothesis (H0): The population of offspring have an equal probability of inheriting all possible genotypic combinations.
- What are the two main types of chi-square tests?
-
The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence.
- What properties does the chi-square distribution have?
-
A chi-square distribution is a continuous probability distribution. The shape of a chi-square distribution depends on its degrees of freedom, k. The mean of a chi-square distribution is equal to its degrees of freedom (k) and the variance is 2k. The range is 0 to ∞.
Sources in this article
We strongly encourage students to use sources in their work. You can cite our article (APA Style) or take a deep dive into the articles below.
This Scribbr articleTurney, S. (July 9, 2022). Chi-Square Goodness of Fit Test | Formula, Guide & Examples. Scribbr. Retrieved October 17, 2022, from https://www.scribbr.com/statistics/chi-square-goodness-of-fit/